Silent Journey Fractal Programs

Quick links: none at the moment.

In fall 2014, I was in 8th grade and was teaching myself to code in Processing, a language based on Java that makes it easy to do graphics without getting bogged down in the technical weeds. In math class, we learned about the Sierpiński triangle, a simple fractal constructed by taking a triangle, connecting the midpoints of its sides to form three smaller right side up triangles and one upside down triangle, and repeating recursively with all the new right side up triangles. We saw how this shape could also be created by a seemingly completely different process called the chaos game: take the original triangle and some random point, draw a new point halfway between this point and a random one of the triangle’s vertices, and repeat. This seemed like the perfect task for Processing: graphical and repetitive. So I coded it up, added some animation and interactivity, and got something like the top-left figure in the collection above. This motivated me to make more interactive fractals in Processing:

1. Sierpiński Triangle Chaos Game. See above.
   

2. Barnsley Fern. In a library book on fractals, I found a more complicated chaos game-style algorithm that produced a fern.
   

3. Koch Curve. The Koch Curve is a well-known fractal created by starting with a line segment, bending up the middle half of that segment to create a triangle, then recursively applying the same procedure to the new segments created.
   

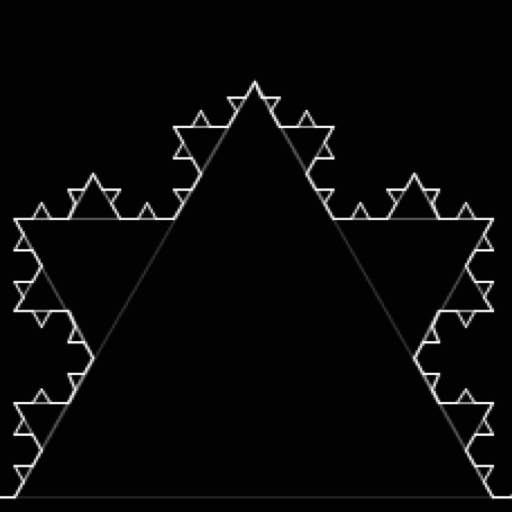
4. Sierpiński Mountain. I read about how one technique for generating images that looked natural involved creating something like a Sierpiński triangle but randomly perturbing each new vertex as it was drawn. My source said this was supposed to look like a mountain; in my implementation, I thought it looked more like a crumpled up piece of paper.
   

5. Mandelbrot Fractal. The Mandelbrot set is perhaps the most famous fractal. I still remember trying to fix a stubborn bug in this one.
   

6. Tree Fractal. A simple fractal created by drawing a “trunk” segment, drawing two branches at the end of the trunk with set angles and sizes relative to the trunk, then taking those branches to be trunks to draw more branches at the end of them, etc. I thought my version looked more like a brain than a tree.
   

I showed my programs to my math teacher, who projected them on a wall during an open house for parents called the Silent Journey. My success with these fractal visualizations inspired me to continue doing cool things with code.